Interpolating 3D
Problems taken from Numerical Computation taught by Elizabeth Bradley.
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from mpl_toolkits.mplot3d import Axes3D
import pandas as pd
from scipy.interpolate import griddata as gd
from pykrige.ok import OrdinaryKriging
from matplotlib import cm
from IPython.display import Image
%pylab inline
Populating the interactive namespace from numpy and matplotlib
Problem 1
Here are some \((x, y, z)\) coordinates for \(22\) points on the Worthington glacier near Valdez, Alaska - twelve on the top and ten on the bottom:
top = np.array([
[33.44, 87.93, 105.88],
[8.81, 84.07, 103.11],
[15.62, 34.83, 105.98],
[40.16, 38.71, 108.13],
[61.45, 67.07, 108.12],
[58.81, 91.44, 107.72],
[36.97, 63.29, 107.14],
[64.71, 42.38, 109.07],
[89.11, 46.49, 109.93],
[67.24, 18.32, 109.99],
[65.90, 31.93, 109.51],
[76.55, 44.51, 109.91]])
bot = np.array([
[15.59, 35.07, 12.88],
[38.57, 37.17, 13.33],
[61.10, 67.15, 17.31],
[58.97, 92.05, 19.09],
[36.98, 63.24, 16.51],
[64.45, 42.66, 20.01],
[89.18, 46.85, 27.71],
[66.87, 18.48, 14.24],
[65.90, 31.93, 21.0],
[76.55, 44.51, 22.0]])
Plot the points on the top surface using your favorite 3D plotting tool. Repeat for the bottom set. Notice how changing the perspective affects your ability to make any sense of the surface from the points. Try connecting the points in a wireframe plot.
First the top
fig = plt.figure(figsize=(8, 8))
ax = fig.add_axes([0.1, 0.1, 0.8, 0.8], projection='3d')
ax.scatter(top[:, 0], top[:, 1], top[:, 2])
for i in range(len(top)):
ax.plot(np.array([0, top[i, 0]]), np.array([top[i, 1], top[i, 1]]),
np.array([top[i, 2], top[i, 2]]), 'k--', alpha=0.3)
ax.plot(np.array([top[i, 0], top[i, 0]]), np.array([0, top[i, 1]]),
np.array([top[i, 2], top[i, 2]]), 'k--', alpha=0.3)
ax.plot(np.array([top[i, 0], top[i, 0]]), np.array([top[i, 1], top[i, 1]]),
np.array([0, top[i, 2]]), 'k--', alpha=0.3)
ax.view_init(azim=30, elev=40)
plt.show()
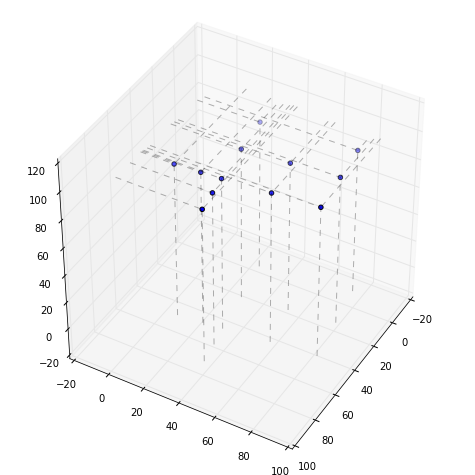
Now the bottom
fig = plt.figure(figsize=(8, 8))
ax = fig.add_axes([0.1, 0.1, 0.8, 0.8], projection='3d')
ax.scatter(bot[:, 0], bot[:, 1], bot[:, 2])
for i in range(len(bot)):
ax.plot(np.array([0, bot[i, 0]]), np.array([bot[i, 1], bot[i, 1]]),
np.array([bot[i, 2], bot[i, 2]]), 'k--', alpha=0.3)
ax.plot(np.array([bot[i, 0], bot[i, 0]]), np.array([0, bot[i, 1]]),
np.array([bot[i, 2], bot[i, 2]]), 'k--', alpha=0.3)
ax.plot(np.array([bot[i, 0], bot[i, 0]]), np.array([bot[i, 1], bot[i, 1]]),
np.array([0, bot[i, 2]]), 'k--', alpha=0.3)
ax.view_init(azim=30, elev=40)
plt.show()

Problems 2 & 3
Using whatever smooth surface interpolation function is available fit a surface to the top points. The surface may pass through the points, or not.
Plot your interpolated surface in 3D, experimenting with shading, point size, and other plotting parameters - contour versus perspective plot, various shading or coloring schemes, etc. - until it looks as good as possible. Turn in a printout of this plot, together with a one-paragraph discussion of your results and observations, including at least a few sentences on how and why you added interpolated points between those in the data set
Using python we have access to griddata which is a simple
interpolation algorithm designed to give a surface based off of a couple
points. This method is great for connected points, however the results
are generally not as detailed as we desire. We will be using this to
connect interpolated points however. This has one parameter for us to
tweak, and that is the interpolation method which can be linear,
cubic, or nearest. For this analysis we will solely use cubic.
The general method used in each interpolation method is to use some
implemented interpolation method to estimate the values of many
intermediate points and then tie everything together with griddata.
Nearest Neighbor Weighted Interpolationn
The first method implemented and examined is Nearest Neighbor Weighted Interpolation, which produces the below images.
This method uses each point in the dataset to determine where the interpolated point should be. Each point in the dataset is weighted based on proximity to the interpolated point and then factored in to its final value. This interpolation process can be expressed as the following equation for some \((x, y)\) pair to be interpolated. (See http://paulbourke.net/miscellaneous/interpolation/ as reference)
\[z = \begin{cases} \frac{\sum\_{i = 1}\^{N - 1} \frac{z\_i}{ {\left\[ {(x\_i - x)}\^2 + {(y\_i - y)}\^2 \right\]}\^{p / 2} } }{\sum\_{i = 1}\^{N - 1} \frac{1}{ {\left\[ {(x\_i - x)}\^2 + {(y\_i - y)}\^2 \right\]}\^{p / 2} } } & \quad x\_i \neq x \text{ or } y\_i \neq y\\ z\_i & \quad x\_i = x \text{ and } y\_i = y \end{cases}\]There are two parameters that can be tweaked in this method in order to
get a "more realistic" surface. The first is the \(p\)
value, which generally determines the relative importance of distant
samples. The second is the interpolation interval. A larger interval
means that fewer points are estimated, and then griddata can make the
surface smooth. In these images values of p = 2 and i = 30 are used.
This method actually has the "nicest" looking surfaces out of all the methods used. These surfaces are the smoothest, and have a nice feel to them. There are no spikes, no skips, nothing to suggest that the data was interpolated.
Image(filename='snaps__top_nearest.png')

Image(filename='snaps__bot_nearest.png')
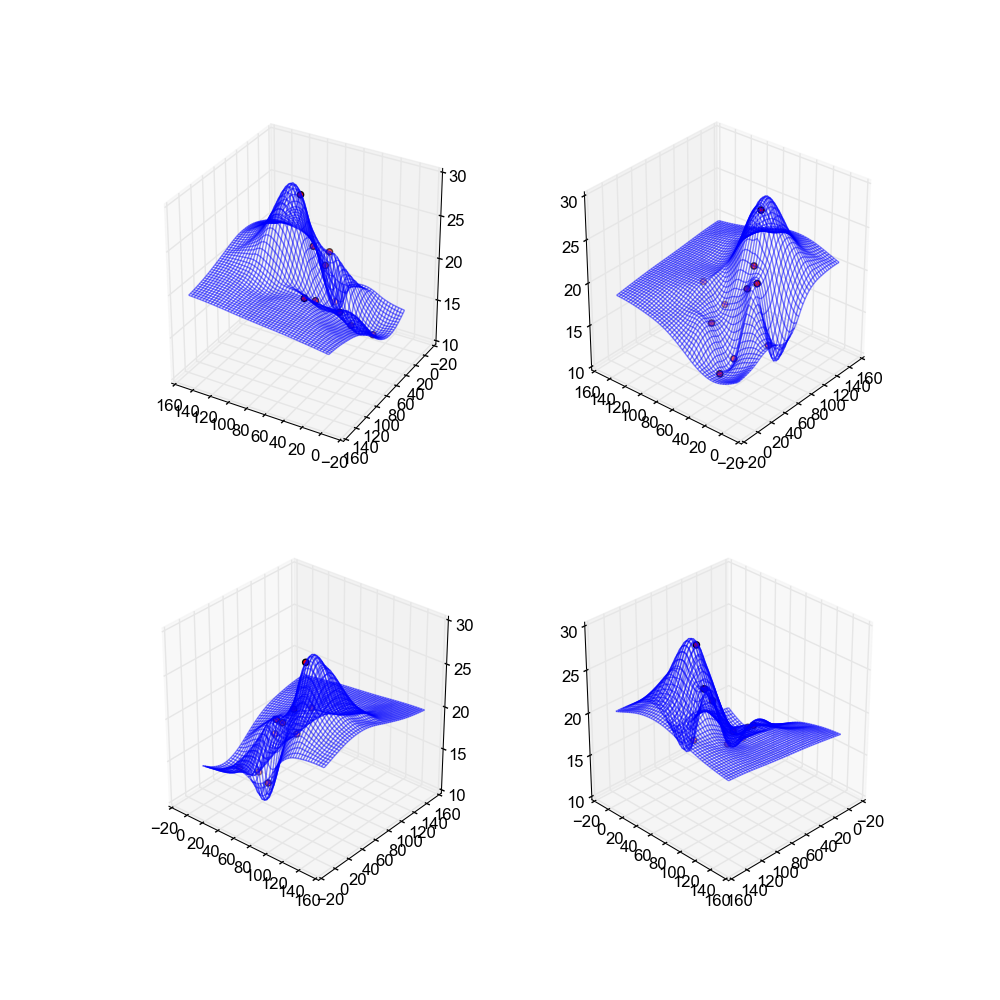
Image(filename='snaps__both_nearest.png')

Kriging
The second method used is kriging. Kriging uses a probabilistic model to determine what the value of \(z\) is at the specified point based on what is most likely. To be entirely honest, an implmentation of this was beyond the scope of the analysis, and I don't have the statistical skills necessary to explain the process well. For a better understanding please reference this paper: http://people.ku.edu/~gbohling/cpe940/Kriging.pdf. In the implementation I used the opensource code available here: https://github.com/bsmurphy/PyKrige.
These surfaces are very "spiky" due to the krigin process, and as a result are limited in their usability. They look nice, and the end result is somewhat decent, however in general these surfaces do not look realistic and are not recommendable.
Image(filename='snaps__top_kriging.png')
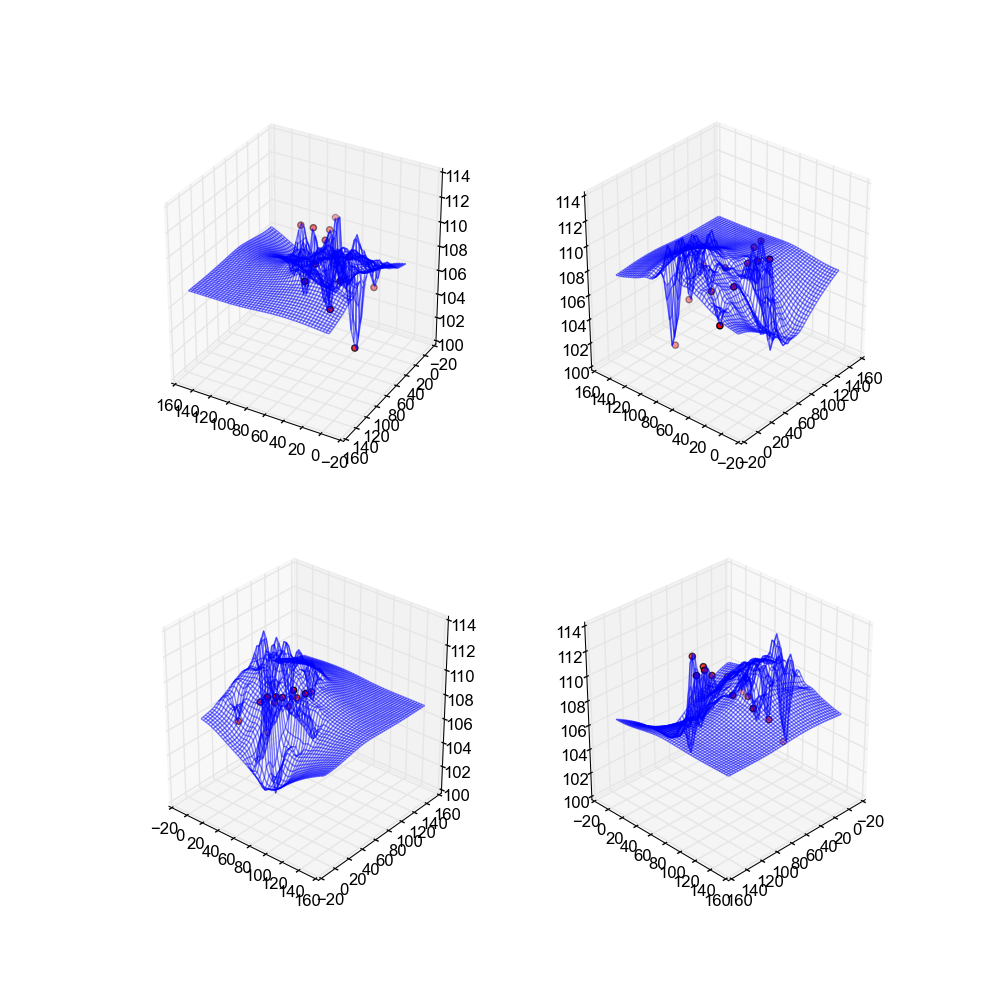
Image(filename='snaps__bot_kriging.png')

Image(filename='snaps__both_kriging.png')

Neural Net
The last method used is a neural net. Neural nets try to simulate the human brain on a much smaller scale through a series of nodes and weighted edges. Please reference this site: http://pages.cs.wisc.edu/~bolo/shipyard/neural/local.html for an introduction to neural networks.
Instead of implementing my own neural net I used PyBrain, available
from this repository: https://github.com/pybrain/pybrain. This library
strives to make neural nets accessible and easy to use.
In my implementation there are two tweakable parameters. The first is how many hidden layers in the network exist, and the second is how many times we train the network on the dataset. In the below images we are using 10 hidden layers and we train the network until the error converges.
If you'll note these surfaces arguable are the worst from any implementation. This is due to the fact that neural networks generally work best when they have a large amount of data off of which to train, and our data sets only have a handful of points. This results in a bad approximation as there just isn't enough to go on.
Image(filename='snaps__top_neural_net.png')

Image(filename='snaps__bot_neural_net.png')

Image(filename='snaps__both_neural_net.png')

Appendix A: Problem 2 & 3 Complete Code
#!/usr/bin/env python2
import sys
from pykrige.ok import OrdinaryKriging
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from matplotlib import cm
from mpl_toolkits.mplot3d import axes3d
from scipy.interpolate import griddata as gd
import pybrain.datasets as pd
from pybrain.tools.shortcuts import buildNetwork
from pybrain.supervised.trainers import BackpropTrainer
top = np.array([
[33.44, 87.93, 105.88],
[8.81, 84.07, 103.11],
[15.62, 34.83, 105.98],
[40.16, 38.71, 108.13],
[61.45, 67.07, 108.12],
[58.81, 91.44, 107.72],
[36.97, 63.29, 107.14],
[64.71, 42.38, 109.07],
[89.11, 46.49, 109.93],
[67.24, 18.32, 109.99],
[65.90, 31.93, 109.51],
[76.55, 44.51, 109.91]])
bot = np.array([
[15.59, 35.07, 12.88],
[38.57, 37.17, 13.33],
[61.10, 67.15, 17.31],
[58.97, 92.05, 19.09],
[36.98, 63.24, 16.51],
[64.45, 42.66, 20.01],
[89.18, 46.85, 27.71],
[66.87, 18.48, 14.24],
[65.90, 31.93, 21.0],
[76.55, 44.51, 22.0]
])
# 'nearest', 'linear', 'cubic'
interpolationmethod = 'cubic'
p = 2
extrapolation_interval = 30
def main():
extrapolation_spots = get_plane(0, 200, 0, 200, extrapolation_interval)
nearest_analysis(extrapolation_spots)
kriging_analysis(extrapolation_spots)
neural_analysis(extrapolation_spots)
def neural_analysis(extrapolation_spots):
top_extra = neural_net(extrapolation_spots, top)
gridx_top, gridy_top, gridz_top = interpolation(top_extra)
plot(top, gridx_top, gridy_top, gridz_top, method='snaps',
title='_top_neural_net')
bot_extra = neural_net(extrapolation_spots, bot)
gridx_bot, gridy_bot, gridz_bot = interpolation(bot_extra)
plot(bot, gridx_bot, gridy_bot, gridz_bot, method='snaps',
title='_bot_neural_net')
plot(np.concatenate((top, bot)), [gridx_top, gridx_bot],
[gridy_top, gridy_bot],
[gridz_top, gridz_bot], method='snaps',
title='_both_neural_net', both=True)
def neural_net(extrapolation_spots, data):
net = buildNetwork(2, 10, 1)
ds = pd.SupervisedDataSet(2, 1)
for row in top:
ds.addSample((row[0], row[1]), (row[2],))
trainer = BackpropTrainer(net, ds)
trainer.trainUntilConvergence()
new_points = np.zeros((len(extrapolation_spots), 3))
new_points[:, 0] = extrapolation_spots[:, 0]
new_points[:, 1] = extrapolation_spots[:, 1]
for i in range(len(extrapolation_spots)):
new_points[i, 2] = net.activate(extrapolation_spots[i, :2])
combined = np.concatenate((data, new_points))
return combined
def nearest_analysis(extrapolation_spots):
top_extra = extrapolation(top, extrapolation_spots, method='nearest')
bot_extra = extrapolation(bot, extrapolation_spots, method='nearest')
gridx_top, gridy_top, gridz_top = interpolation(top_extra)
plot(top, gridx_top, gridy_top, gridz_top, method='snaps',
title='_top_nearest')
gridx_bot, gridy_bot, gridz_bot = interpolation(bot_extra)
plot(bot, gridx_bot, gridy_bot, gridz_bot, method='snaps',
title='_bot_nearest')
plot(np.concatenate((top, bot)), [gridx_top, gridx_bot],
[gridy_top, gridy_bot],
[gridz_top, gridz_bot], method='snaps', title='_both_nearest',
both=True)
def kriging_analysis(extrapolation_spots):
top_extra = extrapolation(top, extrapolation_spots, method='kriging')
bot_extra = extrapolation(bot, extrapolation_spots, method='kriging')
gridx_top, gridy_top, gridz_top = interpolation(top_extra)
plot(top, gridx_top, gridy_top, gridz_top, method='snaps',
title='_top_kriging')
gridx_bot, gridy_bot, gridz_bot = interpolation(bot_extra)
plot(bot, gridx_bot, gridy_bot, gridz_bot, method='snaps',
title='_bot_kriging')
plot(np.concatenate((top, bot)), [gridx_top, gridx_bot],
[gridy_top, gridy_bot],
[gridz_top, gridz_bot], method='snaps', title='_both_kriging',
both=True)
def nearest_neighbor_interpolation(data, x, y, p=0.5):
"""
Nearest Neighbor Weighted Interpolation
http://paulbourke.net/miscellaneous/interpolation/
http://en.wikipedia.org/wiki/Inverse_distance_weighting
:param data: numpy.ndarray
[[float, float, float], ...]
:param p: float=0.5
importance of distant samples
:return: interpolated data
"""
n = len(data)
vals = np.zeros((n, 2), dtype=np.float64)
distance = lambda x1, x2, y1, y2: (x2 - x1)**2 + (y2 - y1)**2
for i in range(n):
vals[i, 0] = data[i, 2] / (distance(data[i, 0], x, data[i, 1], y))**p
vals[i, 1] = 1 / (distance(data[i, 0], x, data[i, 1], y))**p
z = np.sum(vals[:, 0]) / np.sum(vals[:, 1])
return z
def get_plane(xl, xu, yl, yu, i):
xx = np.arange(xl, xu, i)
yy = np.arange(yl, yu, i)
extrapolation_spots = np.zeros((len(xx) * len(yy), 2))
count = 0
for i in xx:
for j in yy:
extrapolation_spots[count, 0] = i
extrapolation_spots[count, 1] = j
count += 1
return extrapolation_spots
def kriging(data, extrapolation_spots):
"""
https://github.com/bsmurphy/PyKrige
NOTE: THIS IS NOT MY CODE
Implementing a kriging algorithm is out of the scope of this homework
Using a library. See attached paper for kriging explanation.
"""
gridx = np.arange(0.0, 200, 10)
gridy = np.arange(0.0, 200, 10)
# Create the ordinary kriging object. Required inputs are the X-coordinates of
# the data points, the Y-coordinates of the data points, and the Z-values of the
# data points. If no variogram model is specified, defaults to a linear variogram
# model. If no variogram model parameters are specified, then the code automatically
# calculates the parameters by fitting the variogram model to the binned
# experimental semivariogram. The verbose kwarg controls code talk-back, and
# the enable_plotting kwarg controls the display of the semivariogram.
OK = OrdinaryKriging(data[:, 0], data[:, 1], data[:, 2], variogram_model='spherical',
verbose=False, nlags=100)
# Creates the kriged grid and the variance grid. Allows for kriging on a rectangular
# grid of points, on a masked rectangular grid of points, or with arbitrary points.
# (See OrdinaryKriging.__doc__ for more information.)
z, ss = OK.execute('grid', gridx, gridy)
return gridx, gridy, z, ss
def extrapolation(data, extrapolation_spots, method='nearest'):
if method == 'kriging':
xx, yy, zz, ss = kriging(data, extrapolation_spots)
new_points = np.zeros((len(yy) * len(zz), 3))
count = 0
for i in range(len(xx)):
for j in range(len(yy)):
new_points[count, 0] = xx[i]
new_points[count, 1] = yy[j]
new_points[count, 2] = zz[i, j]
count += 1
combined = np.concatenate((data, new_points))
return combined
if method == 'nearest':
new_points = np.zeros((len(extrapolation_spots), 3))
new_points[:, 0] = extrapolation_spots[:, 0]
new_points[:, 1] = extrapolation_spots[:, 1]
for i in range(len(extrapolation_spots)):
new_points[i, 2] = nearest_neighbor_interpolation(data,
extrapolation_spots[i, 0],
extrapolation_spots[i, 1], p=p)
combined = np.concatenate((data, new_points))
return combined
def interpolation(data):
gridx, gridy = np.mgrid[0:150:50j, 0:150:50j]
gridz = gd(data[:, :2],data[:, 2], (gridx, gridy),
method=interpolationmethod)
return gridx, gridy, gridz
def plot(data, gridx, gridy, gridz, method='rotate', title='nearest', both=False):
def update(i):
ax.view_init(azim=i)
return ax,
if method == 'rotate':
fig = plt.figure()
ax = fig.add_axes([0.1, 0.1, 0.8, 0.8], projection='3d')
ax.plot_wireframe(gridx, gridy, gridz, alpha=0.5)
ax.scatter(data[:, 0], data[:, 1], data[:, 2], c='red')
animation.FuncAnimation(fig, update, np.arange(360 * 5), interval=1)
plt.show()
elif method== 'snaps':
fig = plt.figure(figsize=(10, 10))
angles = [45, 120, 220, 310]
if both:
for i in range(4):
ax = fig.add_subplot(2, 2, i, projection='3d')
ax.plot_wireframe(gridx[0], gridy[0], gridz[0], alpha=0.5)
ax.plot_wireframe(gridx[1], gridy[1], gridz[1], alpha=0.5)
ax.scatter(data[:, 0], data[:, 1], data[:, 2], c='red')
ax.view_init(azim=angles[i])
else:
for i in range(4):
ax = fig.add_subplot(2, 2, i, projection='3d')
ax.plot_wireframe(gridx, gridy, gridz, alpha=0.5)
ax.scatter(data[:, 0], data[:, 1], data[:, 2], c='red')
ax.view_init(azim=angles[i])
plt.savefig('snaps_{}.png'.format(title))
elif method == 'contour':
fig = plt.figure()
ax = fig.add_axes([0.1, 0.1, 0.8, 0.8], projection='3d')
ax.plot_wireframe(gridx, gridy, gridz, alpha=0.5)
ax.scatter(data[:, 0], data[:, 1], data[:, 2], c='red')
ax.contourf(gridx, gridy, gridz, zdir='z', offset=np.min(data[:, 2]), cmap=cm.coolwarm)
ax.contourf(gridx, gridy, gridz, zdir='x', offset=0, cmap=cm.coolwarm)
ax.contourf(gridx, gridy, gridz, zdir='y', offset=0, cmap=cm.coolwarm)
ax.view_init(azim=45)
plt.show()
if __name__ == '__main__':
sys.exit(main())