Numerical Rootfinding
Bisection Method
import numpy as np
import matplotlib.pyplot as plt
%pylab inline
1. Roots
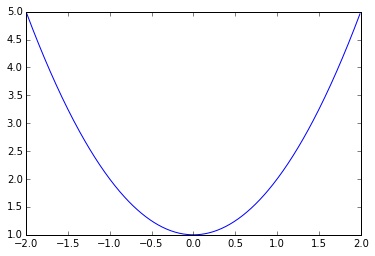
A) Give an example function that has no roots.
$x^2 + 1$
plt.plot(np.arange(-2, 2, 0.01), np.arange(-2, 2, 0.01)**2 + 1)
plt.show()
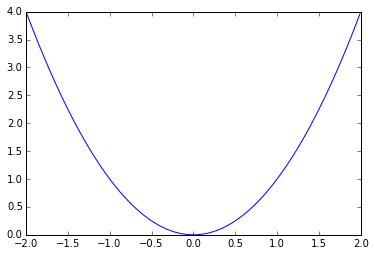
B) Give an example function that has exactly one root.
$x^2$
plt.plot(np.arange(-2, 2, 0.01), np.arange(-2, 2, 0.01)**2)
plt.show()
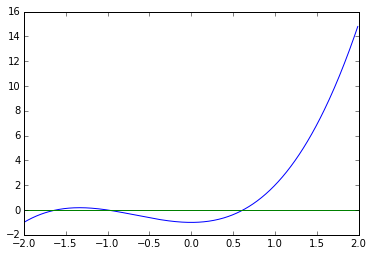
C) Give an example function that has three unique roots.
$x^3 + 2x^2 - 1$
plt.plot(np.arange(-2, 2, 0.01), np.arange(-2, 2, 0.01)**3 + 2 * np.arange(-2, 2, 0.01)**2 - 1)
plt.plot(np.arange(-2, 2, 0.01), np.arange(-2, 2, 0.01) * 0)
plt.show()
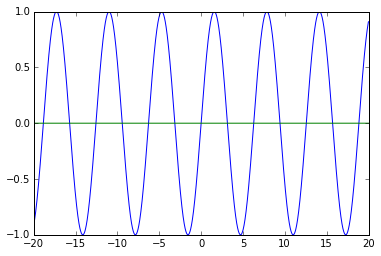
D) Give an example function that has infinite roots.
$\sin(x)$
plt.plot(np.arange(-20, 20, 0.01), np.sin(np.arange(-20, 20, 0.01)))
plt.plot(np.arange(-20, 20, 0.01), np.arange(-20, 20, 0.01) * 0)
plt.show()
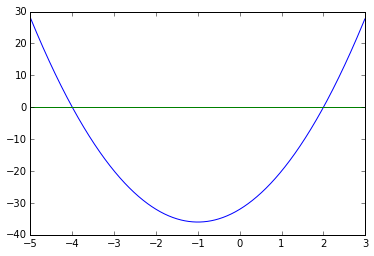
E) How many roots does $4x^2+8x-32$ have?
Exactly 2.
$x = {-4, 2}$
plt.plot(np.arange(-5, 3, 0.01), 4 * np.arange(-5, 3, 0.01)**2 + 8 * np.arange(-5, 3, 0.01) - 32)
plt.plot(np.arange(-5, 3, 0.01), np.arange(-5, 3, 0.01) * 0)
plt.show()
2. The bisection and secant methods for finding roots
A) Write a program that finds a root of the function $f(x) = 2x^3 - x^2 + x - 1$ using the bisection method starting from intial guesses of $x = -4$ and $x = 4$. Note the number of iterations required to get $f(x) < 0.0001$. What happens to that number if the inital guesses are changed to $x=0$ and $x=1$?
We will first write a generic bisection method solver.
def bisectionmethod(f, a, b, steps, precision=1e-4):
m = np.zeros((steps, 2))
m[0, 0] = a
m[0, 1] = b
for i in range(1, steps):
c = (m[i - 1, 0] + m[i - 1, 1]) / 2
if f(c) == 0:
return c, m
elif np.abs(f(a) - f(b)) <= precision:
return c, m
elif f(a) * f(c) < 0:
m[i, 0] = m[i - 1, 0]
m[i, 1] = c
else:
m[i, 0] = c
m[i, 1] = m[i - 1, 1]
return (m[-1, 0] + m[-1, 1]) / 2, m
We will now apply this to our function
f = lambda x: 2 * x**3 - x**2 + x - 1
root, steps = bisectionmethod(f, -4, 4, 100000)
print(root)
print(len(steps.nonzero()[0]))
0.738983621505
105
We can see that we get to $0.0001$ in 2 steps with those initial guesses. Moving on to the second part.
f = lambda x: 2 * x**3 - x**2 + x - 1
root, steps = bisectionmethod(f, -0, 1, 100000)
print(root)
print(len(steps.nonzero()[0]))
0.738983621505
101
We see that this number decreases, but not by much.
Secant Method
B) Write a program that finds a root of the function $f(x) = 2x^3 - x^2 + x - 1$ using the secant method starting from initial guesses of $x=-4$ and $x=4$. Note the number of iterations required to get $f(x) < 0.0001$.
We start by again creating a generic secant method solver.
def secantmethod(f, x0, x1, steps):
m = np.zeros((steps, 2))
m[0, 0] = x0
m[0, 1] = x1
for i in range(1, steps):
c = (m[i - 1, 1] - f(m[i - 1, 1]) *
((m[i - 1, 1] - m[i - 1, 0]) / (f(m[i - 1, 1]) - f(m[i - 1, 0]))))
m[i, 0] = m[i - 1, 1]
m[i, 1] = c
if np.abs(m[i, 1] - m[i, 0]) < 0.001:
break
return c, m
We can now apply this to our equation.
f = lambda x: 2 * x**3 - x**2 + x - 1
root, steps = secantmethod(f, -4, 4, 100000)
print(root)
print(len(steps.nonzero()[0]))
0.738983511089
16
We note it now takes $16$ iterations.
C) Compare the time-to-convergence values that you determined in the first two parts of this problem for the bisection and secant methods. Are these numbers consistent with what you know about the theoretical convergences rates of these two methods?
Yes. We note that in the first part we theoretically have a linear convergence rate, while the secant method is hypothetically superlinear. Examining the number of iterations needed to be fairly precise we can see that there is an order of magnitude difference in the number of iterations required. The secant method is much much faster, which supports the theoretical convergence rates for these two algorithms.
Fixed Point Method
3. Apply the fixed-point method to $f(x) = 2x^3 - x - 1$ starting from an intial guess of $x=1.1$. Try a number of rearrangements of this function until you find at least one for which the iteration sequence converges and at least one for which it doesn’t. What determines whether a given rearrangment will lead to a convergent sequence of iterations?
We again will first create a generic fixed point method function.
def fixedpointmethod(f, x0, steps):
m = np.zeros(steps)
m[0] = x0
for i in range(1, steps):
m[i] = f(m[i - 1])
if np.abs(m[i] - m[i - 1]) < 0.0001:
break
return m[-1], m
We can now apply it to our function rewritten in various forms.
f = lambda x: 2 * x**3 - 1
print(fixedpointmethod(f, 1.1, 1000)[0] == inf)
f = lambda x: ((x + 1) / 2) ** (1/3)
fixedpointmethod(f, 1.1, 1000)[1][:10]
True
array([ 1.1 , 1.01639636, 1.00272529, 1.00045401, 1.00007566,
0. , 0. , 0. , 0. , 0. ])
We can see that the form
\[x = g(x) = 2x^3 - 1\]diverges very quickly, while the form
\[x= g(x) = \sqrt[\leftroot{-2}\uproot{2}3]{\frac{x + 1}{2} }\]converges quickly to zero.
Using a cobweb diagram of these different forms we can see the reason why some converge and some don’t, which is also heavily depedent on the slope of $g^\prime$.
Newton’s Method
import numpy as np
import matplotlib.pyplot as plt
import scipy.misc as sm
%pylab inline
1. Newton’s method for finding roots.
Write a program that finds a root of the function $f(x) = x^2 - 1$ using Newton’s method starting from the initial guess $x = -2$. Note the number of iterations required to get $f(x) < 0.0001$.
We first write a generic Newton’s Method Solver.
def newtonsmethod(f, x0, steps, precision=1e-4):
m = np.zeros(steps)
m[0] = x0
for i in range(1, steps):
m[i] = m[i - 1] - (f(m[i - 1]) / sm.derivative(f, m[i - 1]))
if np.abs(f(m[i])) < precision:
break
return m[i], len(np.nonzero(m)[0])
Now we plug in our equation and initial guess.
f = lambda x: x**2 - 1
root, iterations = newtonsmethod(f, -2, 1000)
print(root, iterations, f(root))
-1.00000004646 5 9.29222969681e-08
Modify your program to find a root of the function $f(x) = x^3 + x^2 - x - 1$ using Newton’s method starting from the inital guess of $x = -2$. Again, note the number of iterations.
This is simply plugging it in.
f = lambda x: x**3 + x**2 - x - 1
root, iterations = newtonsmethod(f, -2, 1000)
print(root, iterations, f(root))
-1.00697705916 77 -9.76983477896e-05
Compare the time-to-convergence values that you determined in the first two parts of this problem for Newton’s method on these two polynomials. Are these numbers consistent with what you know about the theoretical convergence rates of this method?
These numbers are consistent, as Newton’s Method has quadratic convergence.
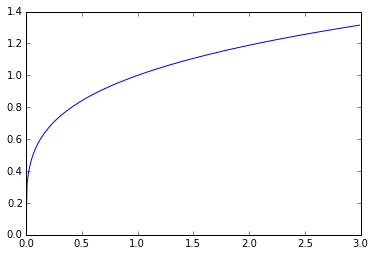
Draw a function $f(x)$ that has exactly one root, but one that Newton’s method won’t be able to find from a subset of initial guesses. Explain why that happens.
Using the equation $f(x) = x^{1/4}$, we can plug it in to our solver.
f = lambda x: x**(1 / 4)
plt.plot(np.arange(0, 3, 0.01), f(np.arange(0, 3, 0.01)))
plt.show()
root, iterations = newtonsmethod(f, 1, 1000)
print(root, iterations, f(root))
nan 1000 nan
This diverges because the behavior near $x = 0$ causes our solver to overshoot as the slope of the line at that point is infinite.
2. Explain what it means for a rootfinder to be quadratically convergent.
If a rootfinder is quadratically convergent than this means that there exists some $C$ such that the following inequality holds.
\[| x_{n + 1} - r | \le C {| x_n - r |}^2\]